Risk Management Research Article

Risk Management

 

Table of Content

Sr.

Title

Page No.1.

Executive Summary2.

Introduction 

Literature Review

Empirical Results

Conclusion 

References 

Appendix 

DOWNLOAD COMPLETE ARTICLE

Risk Management Research Analysis

 

Executive Summary

The danger of borrowers defaulting on their loan obligations is referred to as credit risk. A huge number of institutions have created sophisticated risk quantification, aggregation, and management systems and models in recent years. These models' outputs are also becoming more essential in risk management and performance monitoring processes at banks. We attempt to address the issue of short-term loan default prediction for a Tunisian commercial bank in this research. From 2003 to 2006, we used a database of 924 credit records given to Tunisian businesses by a Tunisian commercial bank. The findings of the K-Nearest Neighbor classifier technique show that the best information set is related to accrual and cash-flow, and the good classification rate is in the order of 88.63 percent (for k=3). To analyze the model's performance, a ROC curve is plotted. The AUC (Area Under Curve) criterion for the first model is 87.4 percent, 95 percent for the third model, and 95.6 percent for the best model incorporating cash flow information.

 

Introduction

The assessment of bank credit risk is frequently utilized by banks all around the world. Because credit risk assessment is so important, a variety of methods are employed to determine risk levels. Furthermore, one of the financial community's primary tasks is credit risk management (Serval, 2008). Credit risk is defined by the Basel Committee on Banking Supervision as the risk that a bank borrower or counterparty may fail to meet agreed-upon obligations. Clients are classified by their profile by banks. Customers' financial backgrounds and subjective criteria are assessed during the classification process. Financial ratios are crucial in determining risk levels (Berk et al., 2011). These are objective ratios that show the financial statement of a company. Financial documents such as the balance sheet, income statement, and cash flow statement are used to gather data for calculating objective financial ratios. There are numerous more subjective criteria, which are dependent on the bank's decision-making approach and mission (Berk et al., 2011).

In a consulting document, the Basel Committee on Banking Supervision attempted to provide guidance to banks and supervisors on appropriate credit risk assessment and valuation policies and practices for loans, regardless of the accounting methodology used. A bank's policies should correctly address validation of any internal credit risk assessment models, according to the third principle in this article. This principle's implementation turns out to be a daily decision based on a binary classification issue that distinguishes excellent payers from bad payers (Karaa & Krichene, 2012). Clearly, assessing insolvency plays a significant function, as a good evaluation of a borrower's quality can aid in deciding whether or not to issue the sought loans. The Basel Committee suggests using either an external mapping technique or an internal rating system to calculate credit risk capital needs (Karaa & Krichene, 2012).

Although the external mapping strategy is difficult to apply due to the lack of external rating grades, the internal rating approach is straightforward and straightforward to adopt, since many techniques for developing credit-risk assessment models have been proposed in the literature. Furthermore, the subprime mortgage crisis, which has rocked the United States and Europe and revealed the banking sector's vulnerability, has cast doubt on the accuracy and utility of agency ratings (Matoussi & Abdelmoula, 2009). Credit scoring methodologies, in reality, are used to assess both objective and subjective variables. In the 1950s, these methods became popular all across the world (Abramowicz et al., 2003). The collecting of client information is standardized using these ways. Furthermore, the scoring system is used to determine whether or not a loan should be approved. Traditional statistical techniques such as logistic regression (Steenackers & Goovaerts, 1989), multivariate discriminant analysis (MDA) (Altman, 1968), classification trees (Davis et al., 1992), neural network (NN) models (Desai et al., 1996, Matoussi & Abdelmoula, 2009; Karaa and Krichène, 2012), and nonparametric statistical models such as k-nearest neighbour (1997). Bayesian classification rules utilizing Nave Bayes classifiers have been proposed in recent contributions. The findings of these investigations showed that they can often outperform the most commonly used strategies. In this context, bankruptcy prediction models developed by Sarkar and Sriram (2001) and Sun and Shenoy (2007) were successful.

Risk Management Research Analysis

Literature Review

Theoretical Framework of Credit Risk Problem

The formulation of the optimal form of the lending contract is one of the most significant applications of agency theory to the lender-borrower dilemma. There is an information imbalance in the credit market between the borrower, who usually has better information about the investment project and its possible earnings and risks, and the lender (the bank), who does not have enough and reliable information about the investment project. This lack of quantity and quality information causes issues both before and after the transaction. Moral hazard and unfavorable selection are common when asymmetric information is present. A classic principal-agent dilemma can be seen in this scenario. According to the nature of information asymmetry, the principal-agent models of agency theory can be classified into three groups (Karel, 2006). To begin, we look for models that are classified as moral hazard because they have ex-post asymmetric knowledge. After signing the contract, the agent is given some confidential information. Moral hazard happens when an asymmetric information problem arises after a transaction has taken place. Because the borrower possesses information about the project that the lender does not, the lender runs the risk of the borrower engaging in activities that the lender does not want because they make it less likely that the loan will be repaid (Matoussi & Abdelmoula, 2009).

Second, we seek out unfavorable selection models, which have ex-ante asymmetric information (Karel, 2006). Before signing the contract, the agent in these models gets access to personal information. Adverse Selection occurs when a borrower has significant information about the quality of a project that the lender does not (or vice versa) before the transaction takes place. This occurs when the potential borrowers who are most likely to have a negative outcome (poor credit risks) are the most engaged in seeking a loan and hence are the most likely to be chosen. Because the riskiness of projects is unknown, lenders' pricing cannot distinguish between good and bad borrowers in the basic situation. Finally, there is signaling, which is the third class.

This issue has usually been studied within the context of costly state verification, which was first introduced by (Townsend, 1979). The agent, who has no endowment, borrows money from the principal to fund a one-time investment project. A moral hazard issue confronts the agent. Should he report the true value or should he reduce the project's outcome? Ex-post moral hazard is demonstrated in this instance. Furthermore, we may encounter an ex-ante moral hazard situation, in which an agent's unobservable effort during the project implementation may have an impact on the project's outcome. According to Townsend (1979), the best contract for solving this problem is the ordinary (or simple) debt contract. The face value of this conventional debt contract is the amount that the agent must repay once the project is completed. (Diamond, 1984) proposed another theoretical basis for simple debt contracts, in which a costly punishment replaced the costly state verification. Only under the risk neutrality assumption, according to Hellwig (2000, 2001), are the two models comparable. When risk aversion is introduced, the costly state verification model continues to work, but the costly punishment model fails. Credit institutions can deal with the asymmetric information problem and its repercussions on credit risk appraisal in the real world by using either guarantee (collateral) or bankruptcy prediction modelling, or both (Karaa & Krichène, 2012).

Risk Management Research Analysis

Credit Risk Assessment and Bankruptcy Prediction

Following a rash of high-profile bank failures in Asia, regulators have recognized the need for advanced technology to assess credit risk in bank portfolios and have urged banks to use it. Correctly assessing credit risk also allows banks to engineer future lending transactions to meet specific return/risk criteria. Credit risk analysis necessitates the development of reasonably accurate quantitative prediction models that can serve as early warning signals for counterparty defaults. In the literature, a number of researchers presented two primary approaches to credit scoring. The first approach, known as structural or market-based models, was proposed by (Merton, 1974), and is based on modelling the underlying dynamics of interest rates and business characteristics to derive the default probability derivation. Initially, this method is based on the asset value model, which has an endogenous default process and is linked to the firm's capital structure. When the value of a company's assets falls below a certain threshold, it is said to have defaulted (Crouhy et al., 2000).

The second method relies on empirical or accounting-based models, in which the relationship between default likelihood and business characteristics is discovered from data rather than modelled. Some strategies in this area were synthesized by Raymond (2007), Thomas et al. (2002), Galindo and Tamayo (2000). Academics and practitioners have researched bankruptcy prediction extensively, as evidenced by the studies of Beaver (1966) and Altman (1968). There have been several models created and empirically tested. Altman's well-known Z-Score (Altman, 1968) is a linear discriminant analysis model that was used to forecast the likelihood of a corporation defaulting. The Ohlson O-Score (Ohlson, 1980) is based on generalized linear models or multiple logistic regression, which have been used to determine the best predictors of bankruptcy and the prediction accuracy rate of their occurrence. In order to anticipate bankruptcy, neural network models were tweaked and employed (Atya, 2001; Matoussi & Abdelmoula, 2009). With the capacity to incorporate a large number of features in an adaptive nonlinear model, their strong predictive capability makes them a popular choice (Kay & Titterington, 2000).

Many studies have concentrated on non-parametric approaches (e.g., k-nearest neighbour) (Henley & Hand, 1996), decision trees (Quinlan, 1992), and neural networks (Mcculloch & Pitts, 1943). Other classification systems, such as Support Vector Machine, combine various techniques to construct a classification model (e.g., Lee and Chen, 2005; Lee et al., 2002). West (2000) compared the credit scoring accuracy of five Artificial Neural Network models, including multilayer perceptron, radial basis function, fuzzy adaptive resonance, mixture-of-experts, and learning vector quantization. West (2000) employed two real-world data sets, one Australian and the other German, in his research. In order to improve his predictive power, he used tenfold cross validation. Both good and terrible credit rates were mentioned. Finally, he compared the results to those of five other common techniques: linear discriminant analysis, logistic regression, k closest neighbour, kernel density estimation, and decision trees. The findings suggest that multilayer perception may not be the most accurate Artificial Neural Network model, and that credit scoring applications should include both combination-of-experts and radial basis function Neural Network models. In the typical situation, logistic regression is a more accurate and precise method than Neural Network models when compared to older methods.

Despite extensive research into credit scoring, Vera et al. (2012) claim that no consensus exists on the best classification technique to utilize. When comparing the outcomes of different investigations, Baesens et al. (2003b) discovered that certain disputes can occur. However, according to Thomas et al. (2002), most credit scoring techniques function similarly. Indeed, the interpretability and openness of certain procedures may lead banks and financial organizations to choose them (Martens et al., 2009). According to Vera et al. (2002), the predictive performance of credit scoring algorithms, as well as the insights or interpretations offered by the model, are both very essential.

Risk Management Research Analysis

Empirical Research Design

Banks operate in a highly competitive market, so the quality of service provided during credit risk assessment is critical. To obtain a competitive edge, when a customer requests credit from a bank, the bank should examine the request as quickly as feasible (Berk et al., 2011). Furthermore, the same process is repeated for each credit demand, which costs the bank money. Because of the importance of credit risk analysis, financial institutions have created a variety of approaches and models to help them decide whether or not to extend credit (inko, 2006).

Parametric and non-parametric problems are the two types of classification methods. In fact, parametric techniques solve problems by estimating the parameters of distributions based on the assumptions of regularly distributed populations (Zhang et al., 2007). Non-parametric approaches, on the other hand, do not make assumptions about the individual distributions involved, and thus are distribution-free, according to Berry and Linoff (1997). A non-parametric statistical method is exemplified by the k-nearest neighbour classifier. A K-NN classifier searches the pattern space for k training (Pranab & Radha, 2013) instances that are comparable to unknown cases when given an unknown case. The K-nearest neighbours of the unknown cases are the k training cases (Ravinder & Aggarwal, 2011). When the dependent variable has multiple values, such as high risk, medium risk, and low risk, the K-NN classifier can be effective. Furthermore, for optimal performance, the K-NN classifier needs an equal number of good and bad sample examples (Hand & Henley, 1997). The k-NN algorithm's performance is also affected by the choice of k, according to Berry and Linoff (1997). This is something that can be tested. To assess the classifier's error rate, we utilize a test case starting with k=1. Each time, k is increased to accommodate one more neighbour, and the procedure is repeated. It is possible to choose the K-value that yields the lowest mistake rate. The larger the number of training samples, the higher the value of k.

ROC Curve as Performance Classifier

Receiver Operating Characteristics (ROC) is a performance graphing method that is widely used. In other words, a ROC graph is a visual, organizational, and selection approach for classifiers based on their performance. Fawcett is a fictional character who appears in the television series (2006). ROC graphs were first used in machine learning by Spackman (1989). He showed how ROC curves might be used to evaluate and compare algorithms (Fawcett, 2006). ROC graphs have become increasingly popular in the machine learning community in recent years. Because basic classification accuracy is typically an inadequate criterion for assessing performance (Provost & Fawcett, 1997; Provost et al., 1998). They also have characteristics that make them particularly beneficial in areas with skewed class distribution and disproportionate classification mistake costs (Fawcett, 2006).

Risk Management Research Analysis

The performance of a classifier is represented by a ROC curve, which is a two-dimensional graph. To compare classifiers, Fawcett (2006) recommends reducing ROC performance to a single scalar value that represents predicted performance. Many scholars, including Bradley (1997) and Hanley and McNeil (1982), propose calculating the area under the ROC curve, also known as AUC. The AUC is a percentage of the unit square's area, with a value that is always between 0 and 1.0. However, no realistic classifier should have an AUC smaller than 0.5, because random guessing yields the diagonal line between (0, 0) and (1, 1), which has an area of 0.5. (Fawcett, 2006).

Empirical Results

We created three different K-NN classifiers in our experiment. Data on financial ratios is used by the first classifier (cash-flows excluded). Non-cash-flow model will be used to describe it. The second model incorporates information from all ratio indicators (cash-flows included, collateral excluded). The cash-flow model will be used. All of the study's indicators are used in the third model. 'Full information model' will be the term used. The k-nearest neighbour (k-NN) methodology, according to Rafiul et al. (2008), is a simple and intuitively appealing strategy for dealing with classification difficulties because of its interpretable nature. Choosing an acceptable distance function for k-NN, on the other hand, can be difficult, and a poor choice can make the classifier extremely susceptible to data noise. We experimented with a variety of k values in our research (2, 3, 4 and 5). Based on our testing, we determined the best value of k for k-NN, which resulted in the best classification performance, which is presented in the result tables.

k-NN classifier with variation of the parameter k=2

Risk Management Research Analysis

Healthy 

Risky 

Healthy companies

358

100

Risky companies

100

366

% Total Good and Bad Classification

Good classification

78.35%

Bad classification

21.64%

Results for Cash-Flow models

K=2

K=3

K=4

K=5

Healthy

Risky

Healthy

Risky

Healthy

Risky

Healthy

Risky

Healthy

395

63

409

49

387

71

375

83

companies

Risky

59

407

56

410

72

394

92

374

companies

% Total Good and Bad Classification

Good

86.79%

88.63%

84.52%

81.06%

classification

Bad

13.20%

11.37%

15.48%

19.94%

classification

Results for full information models

K=2

K=3

K=4

K=5

Healthy

Risky

Healthy

Risky

Healthy

Risky

Healthy

Risky

Healthy

companies

393

65

406

52

381

77

383

75

Risky

companies

69

397

69

397

99

367

113

353

% Total Good a Good classification

nd Bad Classification

85.5%

86.90%

80.95%

79.65%

Bad

classification

14.50%

13.10%

19.05%

20.35%

The categorization results for both cash flow and complete information models. The classifiers with the best performance are bolded and highlighted in red. Tables 4 and 5 demonstrate that the best model with the best classification rate is the one combining accrual and cash flow data (table 4) with an excellent classification rate of 88.63 percent vs 86.90 percent for the third model with all data. Remember that our goal is to determine the new point's class label. The behaviour of the algorithm varies depending on k, and the value of K in this study was chosen. We can also come to the conclusion that k –NN is the best parameter. The findings were improved by increasing the parameter k to three. The percentage of correctly classified items is improving. Furthermore, when cash flow information is included, the model reduces error type I from 16.73 percent to 12 percent and error type II from 20.52 percent to 10.69 percent.

Criterion of the type I and II error

ERROR

K=2

K=3

K=4

K=5

NON-CASH FLOW MODEL

Type I

21.83%

16.73%

27.51%

27.25%

Type II

21.45%

20.52%

26.18%

27.72%

CASH FLOW MODEL

Type I

12.66%

12.01%

15.45%

19.74%

Type II

13.75%

10.69%

15.50%

18.12%

FULL INFORMATION MODEL

Type I

14.8%

14.80%

21.24%

24.24%

We want to estimate credit risk in this study by employing a set of financial ratios that are commonly used in loan contracts. The predictions on financial ratio selection show the link between financial ratios and credit risk. In the practitioner and academic literature, this evidence is well-known (Demerjian, 2007). Indeed, textbooks emphasize the importance of ratios in evaluating credit quality (Lundholm & Sloan, 2004), and academic research find that when employed as covenants, financial ratios give indications regarding borrower credit risk (Smith & Warner, 1979; Dichev & Skinner, 2002).

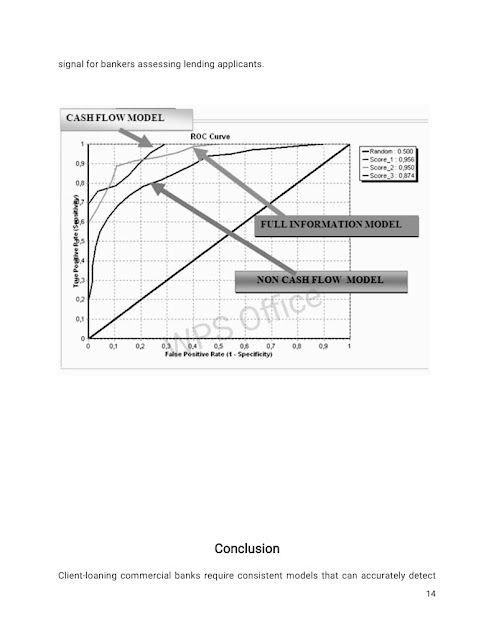
The ROC Curve

A perfect classifier's ROC curve is the curve that follows the two axes and orders all bad cases before good cases. For a given value of the sill, it would classify 100% bad situations as class bad and 0% good ones as class bad. A classifier with a ROC curve that follows the 45° line is ineffective, according to Yang (2002). At each value of the threshold, the same proportion of bad and good cases would be assigned to the class bad; the classes would not be separated. Between these two extremes, real-world classifiers develop ROC curves. The Area Under the ROC Curve (abbreviated as AUC) is a metric that can be used to assess the curve's performance (Hand, 1997). The curve with a higher AUC is preferable than the one with a lower AUC. We can see that the AUC requirement for the best model is around 95.6 percent (cash flow model). This is a good score because it is greater than 50%. This result backs with the preceding section's finding of a high categorization rate. We might conclude that cash flow data is a useful signal for bankers assessing lending applicants.

Conclusion

Client-loaning commercial banks require consistent models that can accurately detect and anticipate defaults. In the current competitive and unpredictable economic environment, Moonasar (2007) stressed that reducing credit risk is one of the most important issues that each bank must deal with. To assess a credit applicant's creditworthiness, we traditionally use scoring systems. In truth, credit scoring is a mathematical tool for assessing creditworthiness (Yang, 2002). Credit scoring is a classification process that divides borrowers into risk groups. Scoring systems are used to estimate the likelihood of a borrower or counterparty defaulting (Komor'ad, 2002). Credit scoring is crucial in assessing credit risk. According to Moonasar (2007), a popular way to credit scoring is to use a classification algorithm using data from prior customers to identify a link between the customers' qualities and their likelihood of defaulting on their debt. Credit scoring systems are used by lenders to evaluate whether applicants are likely to repay their debts. To distinguish between possible good and bad credit applicants, an accurate classifier is required. The best K-NN with k=3 for the three models, and the best global classification rate is in the order of 88.63 percent, according to the primary results. Additionally, a ROC curve is shown to evaluate the model's performance. The AUC requirement is 95.6 percent, according to the results. Our research, on the other hand, is lacking in that it.

 

References

Abid, F. & A. Zouari (2000) “Financial distress prediction using neural networks”, http://ssrn.com/abstract=355980 or DOI: 10.2139/ssrn.355980.

Abramowicz, W. M. Nowak, J. Sztykiel (2003) “Bayesian networks as a decision support tool in credit scoring domain”, Idea Group Publishing

Altman, E. I. (1968) “Financial ratios, discriminant analysis and the prediction of corporate bankruptcy”, Journal of Finance, vol. 23: 589–609

Anderson, D.R., Sweeney, D.J., Freeman, J., Williams T.A. & Shoesmith, E. (2007) “Statistics for business and economics”, London: Thomson Learning EMEA

Antonakis, A. C. & Sfakianakis, M. E. (2009) “Assessing naive bayes as a method for screening credit applicants”, Journal of Applied Statistics, vol. 36: 537-545

Atiya, A.F. (2001) “Bankruptcy prediction for credit risk using neural nets: a survey and new results”, IEEE Transactions on Neural Nets, vol. 12 (4): 929-935

Beaver, W. (1966) “Financial ratios as predictors of failure. Empirical research in accounting: Selected studies”, Journal of Accounting Research, vol. 5: 71–111

Berk Bekiroglu Hidayet Takci1 & Utku Can Ekinci (2011) “Bank credit risk analysis with Bayesian network decision tool” International Journal of Advanced Engineering Sciences and Technologies, vol. 9, no. 2: 273-279

Berry. M.J.A. & Linoff, G.S (1997) Data mining techniques for marketing, sales, and customer support, John Wiley & Sons, Inc.

Berstein, L. A. & Wild J.J. (1998) Financial statement analysis: theory, application, and interpretation, sixth Edition, McGraw-Hill

Bogess, W. P. (1967) “Screen -test your credit risks”, Harvard Business Review, vol. 45, no. 6: 113-122

Bradley, A.P. (1997) “The use of the area under the ROC curve in the evaluation of machine learning algorithms”, Pattern Recogn, vol. 30(7): 1145-1159

Çinko, M. (2006) “Comparison of credit scoring tecniques: Istanbul ticaret üniversitesi sosyal bilimler”, Dergisi, vol. 9: 143-153

Crouhy, M.; Galai, D.; Mark, R. (2000) “A comparative analysis of current credit risk models”, Journal of Banking and Finance, vol. 24, no. 1: 59-117

Davis R. H., Edelman, D.B. & Gammerman, A.J. (1992) “Machine learning algorithms for credit-card applications”, IMA Journal of Management Mathematics, vol. 4: 43-51

Davutyan, N. & Özar, S. (2006) “A credit scoring model for Turkey’s micro & small enterprises (MSE’s),” 13th Annual   ERF   Conference, Kuwait, 16 – 18 December 2006

Demerjian, P. R. W (2007) “Financial ratios and credit risk: the selection of financial ratio covenants in debt contracts”, working paper, workshop Stephen M. Ross School of Business University of Michigan, January 11

Desai, V. S., Crook, J. N. & Overstreet, G. A. (1996) “A comparison of neural networks and linear scoring models in the credit union environment”, European Journal of Operational Research, vol. 95(1): 24–37

Galindo, J. & Tamayo, P. (2000) “Credit risk assessment using statistical and MachineLearning: basic methodology and risk modeling applications”, Computational Economics, vol. 15(1-2): 107- 143

Hand, D. J. (1997) Construction and assessment of classification rules, Wiley series in probability and statistics, John Wiley & Sons

Hand, J. & Henley, W. (1997) “Statistical classification methods in consumer credit scoring”, Computer Journal of the Royal Statistical Society Series a Statistics in Society”, vol. 160, no. 3: 523-541

Hanley, J.A. & McNeil, B.J. (1982) “The meaning and use of the area under a receiver operating characteristic (ROC) curve”, Radiology, vol. 143: 29–36

Hellwig, M. (2000) “Financial intermediation with risk aversion”, Review of Economic Studies, vol. 67(4): 719–742

Hellwig M. (2001) “Risk aversion and incentive compatibility with ex post information Asymmetry”, Economic Theory, vol. 18 (2):415–438.

Henley, W.E. & Hand, D.J. (1997) “Statistical classification methods in consumer credit scoring: a review”, Journal of the Royal Statistical Society. Series A (Statistics in society), vol. 160, no. 3: 523- 541

Karaa,A. & Krichène, A. (2012) “Credit–risk assessment using support vectors machine and multilayer neural network models: a comparative study case of a Tunisian bank”, Accounting and  Management  Information  Systems,  vol. 11, no. 4: 587–620

Karel.J. (2006) “Agency theory approach to the contracting between lender and borrower” Acta Oeconomica Pragensia, 14/3

Kay, J. & Titterington, M. (eds) (2000) “Statistics and Neural Nets, Advances at the Interface”, Oxford University Press

Komorad, K. (2002) “On credit scoring estimation”, Institute for statistics and econometrics, Humboldt University, Berlin

Lee, T. & Chen, I. (2005) “A two-stage hybrid credit scoring model using artificial neural networks and multivariate adaptive regression splines”, Expert Systems with Applications, vol. 28(4): 743–752

Lee, T., Chiu, C., Lu, C. & Chen, I. (2002) “Credit scoring using the hybrid neural discriminant technique”, Expert Systems with Applications, vol. 23(3): 245-254

Lundholm, R. & Sloan, R. (2004) Equity valuation & analysis, New York; McGraw-Hill/Irwin

Matoussi, H. & Krichène Abdelmoula, A. (2010) “Credit risk evaluation of a Tunisian commercial: Bank: logistic regression versus Neural Network Modelling”, Accounting and Management Information Systems, vol. 9, no. 1

Matoussi, H., Mouelhi, R. & Salah, S. (1999) “La prédiction de faillite des entreprises tunisiennes par la régression logistique”, Revue Tunisienne des Sciences de Gestion, vol. 1: 90-106

Mcculloch, W. & Pitts, W. (1943) “A logical calculus of the ideas immanent in nervous activity”, Bulletin of Mathematical Biophysic, vol. 5: 115-133

Merton, R. (1974) “On the pricing of corporate debt: The risk structure of interest rates,” Journal of Finance, vol. 29: 449-470

Mileris, R. (2010) “Estimation of loan applicants default probability applying discriminant analysis and simple Bayesian classifier”, Economics and Management, vol. 15: 1078-1084

Moonasar, V. (2007) “Credit risk analysis using artificial intelligence: evidence from a leading South African banking institution”, Research Report: Mbl3

Ohlson, J. A. (1980) “Financial ratios and the probabilistic prediction of bankruptcy”, Journal of Accounting Research, vol. 18: 109-131

Palepu K.G., Healy, P.M. & Bernard, V.L. (2000) Business analysis & valuation using financial Statements, second Edition, South – Western College Publishing

Pranab Kumar D. G., Radha Krishna, P., (2013) «Database management system oracle SQL AND PL/SQL” PHI Learning Pvt. Ltd., 576 pages

Provost, F. & Fawcett, T. (1997) “Analysis and visualization of classifier performance: Comparison under imprecise class and cost distributions”, In: Proc. Third Internat. Conf. on Knowledge Discovery and Data Mining (KDD-97). AAAI Press, Menlo Park

Provost, F., Fawcett, T. & Kohavi, R. (1998) “The case against accuracy estimation for comparing induction algorithms”, In: Shavlik, J. (Ed.) Proc. ICML-98. Morgan Kaufmann, San Francisco, Available from: <http://www.purl.org/ NET/tfawcett/papers/ICML98-final.ps.gz>.

Quinlan, J. R. (1992) C4.5 “programs for machine learning”, Morgan Kaufmann Publishers Inc., California

Raymond, A. (2007) The Credit Scoring Toolkit: Theory and Practice for Retail Credit Risk Management and Decision Automation, Oxford University Press, United States of America, 1st edition.

Revsine, L., Collins, D.W. & Johnson, W.B. (1999) Financial Statement and Analysis, Prentice Hall, New Jersey.

Rosner, B.A. (2006) Fundamental of Biostatistics, Taunton: Quebecor World Rumelhart, D.E., Hinton, G.E. & McClelland, J.L. (1986) “A general framework for parallel distributed processing”, In “Parallel Distributed Processing: explorations in the microstructure of cognition”, vol. 1, pp. 45-75

Sarkar, S. & Sriram, R.S. (2001) “Bayesian models for early warning of bank failures”, Management Science, vol. 47(11): 1457-1475

Seval, S. (2008) “Credit risk and Basel II”, Credit Risk Solutions Inforsense Smith, C. & Warner, J. (1979) “On financial contracting”, Journal of Financial Economics, vol. 7: 117-161

Spackman, K.A. (1989) “Signal detection theory: Valuable tools for evaluating inductive learning”, In: Proc. Sixth Internat. Workshop on Machine Learning, Morgan Kaufman, San Mateo, CA, pp. 160-163.

Steenackers, A. & Goovaerts, M.J. (1989) “A credit scoring model for personal loans”, Insurance Mathematics and Economics, vol. 8: 31-34

Thomas, L.C. (2002) “A survey of credit and behavioral scoring: forecasting financial risk of lending to consumers”, International Journal of Forecasting, vol. 15: 149-172

Townsend, R. M. (1979) “Optimal contracts and competitive markets with costly state verification”, Journal of Economic Theory, vol.21 (2): 265-293

Vera L. M., Dries F.B. & Van den Poel, D. (2012) “Enhanced decision support in credit scoring using Bayesian binary quantile regression”, Working Paper August

West, D. (2000) “Neural network credit scoring”, Computer & Operations Research, vol. 27 (11): 1131-1152

West, D. (2000) “Neural network credit scoring model”, Computational Operation Research vol. 27: 1131-1152

Yang, L. (2002) “The evaluation of classification models for credit scoring”, Working Paper no. 02/2002 Edit. Matthias Schumann University of Göttingen Institute of computer science

Zhang, D., Huang, H., Chen, Q. & Jiang, Y. (2007) “Comparison of credit scoring models”, Third international conference of Natural Computation, vol. 1

 

Appendix

APPENDIX 1: NON-CASH FLOW MODEL

Panel 1: K-NN with k=2

Panel 2: K-NN with k=3

Panel 3: K-NN with k=4